In 1990, Yann Lecun, a renowned computer scientist who received the ACM A.M. Turing Award in 2018, published a seminal paper titled “Optimal Brain Damage” [1]. Here, Dr. Lecun showed the “Graceful Degradation Property” in DNNs: one can optimally remove 60% of model parameters in a DNN without compromising its performance. Amazing! Isn’t it?
This belief has been harnessed in a broad range of ML techniques that we commonly use today, such as network pruning which reduces up to 90% of parameters in a network without any accuracy drop. Besides structural resilience, researchers found that DNNs can tolerate a small amount of noise in their parameters with minimal accuracy degradation, which results in defensive techniques such as adding Gaussian noise to model parameters to strengthen DNNs against adversarial examples.
Recent work in adversarial machine learning has strengthened this faith in “The Optimal Damage”. Prior work demonstrated that it’s extremely difficult for an adversary to decrease the accuracy of a DNN by more than 10% by blending malicious training data. Another line of work examined whether a DNN can be resilient to storage media errors, e.g., unexpected bitwise errors in the recording devices, but a DNN did not lose more than 5% accuracy when there were 2,600 parameters out of 2.5 million corrupted by random errors. Similarly, researchers also performed the stress tests of a DNN to examine its resilience to bitwise errors; however, their experiments only led to a 7% accuracy drop on average with thousands of random bit-flips.
Well. Could the Damage Be Always Optimal?
Network pruning or defensive techniques focus on identifying model parameters whose perturbations will NOT lead to a significant accuracy loss (best-case scenarios). Research about a DNN’s resilience to bitwise errors measured the averaged accuracy drop over multiple bitwise corruptions, not the consequences from an individual bitwise error (average-case scenarios). However, all these practices lead to a false sense of security.
Let’s look at the bitwise representation of model parameters in a computer. A network’s parameters are commonly represented by single-precision (32-bit) floating-point numbers (as the IEEE-754 format) that use the exponential notation. For example, 0.3504 becomes 1.40 × 2 − 2; 1.40 expresses the mantissa and −2 is the exponent. In the IEEE-753 format, 23 bits are assigned to mantissa, 8 bits for the exponent, and one bit for the sign of the value.
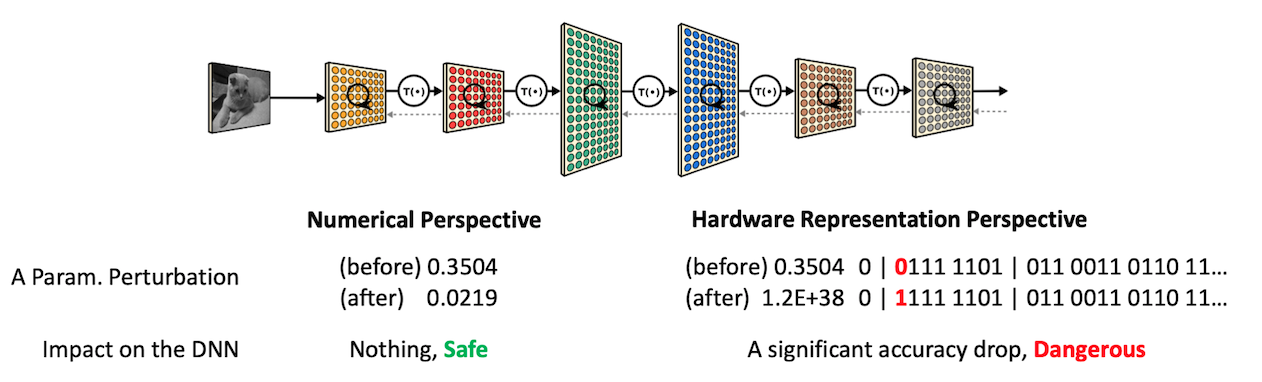
The fact that model parameters are represented in the exponential format provides a different understanding of their resilience to a small amount of perturbation. We show in the left-side how the “Optimal Brain Damage” work considers a perturbation; they see it as a small numerical error to the DNN’s parameters. However, on the right side, our perspective of an atomic error in the same parameter (represented as the IEEE-754 format in a computer) is a single-bit error, which can lead to a significant numerical change of a parameter value.
Huh, But How Vulnerable Are DNNs to Such A Single-Bit Error?
Good question. Indeed, we asked the same question: how vulnerable are DNNs to the atomic perturbation (a single bit-flip)? To answer this, we first define the concept of Achilles-bit.
Here, we choose 10% as our threshold because this was the amount that previous work had a hard time to inflict. Then, we conduct an extensive search of Achilles bits in 19 DNNs. Those are the CNN models trained on 3 popular computer vision datasets (MNIST, CIFAR-10, and ImageNet) We took each model, flipped all the bits in the model one by one, and measured the accuracy of the corrupted model on the test-set after we flip each bit. At the same time, we compute (1) MaxRAD: the maximum accuracy drop that can be caused by a single-bit flip, and (2) the ratio of model parameters that contain at least one Achilles bit. Then, Ta-Da!
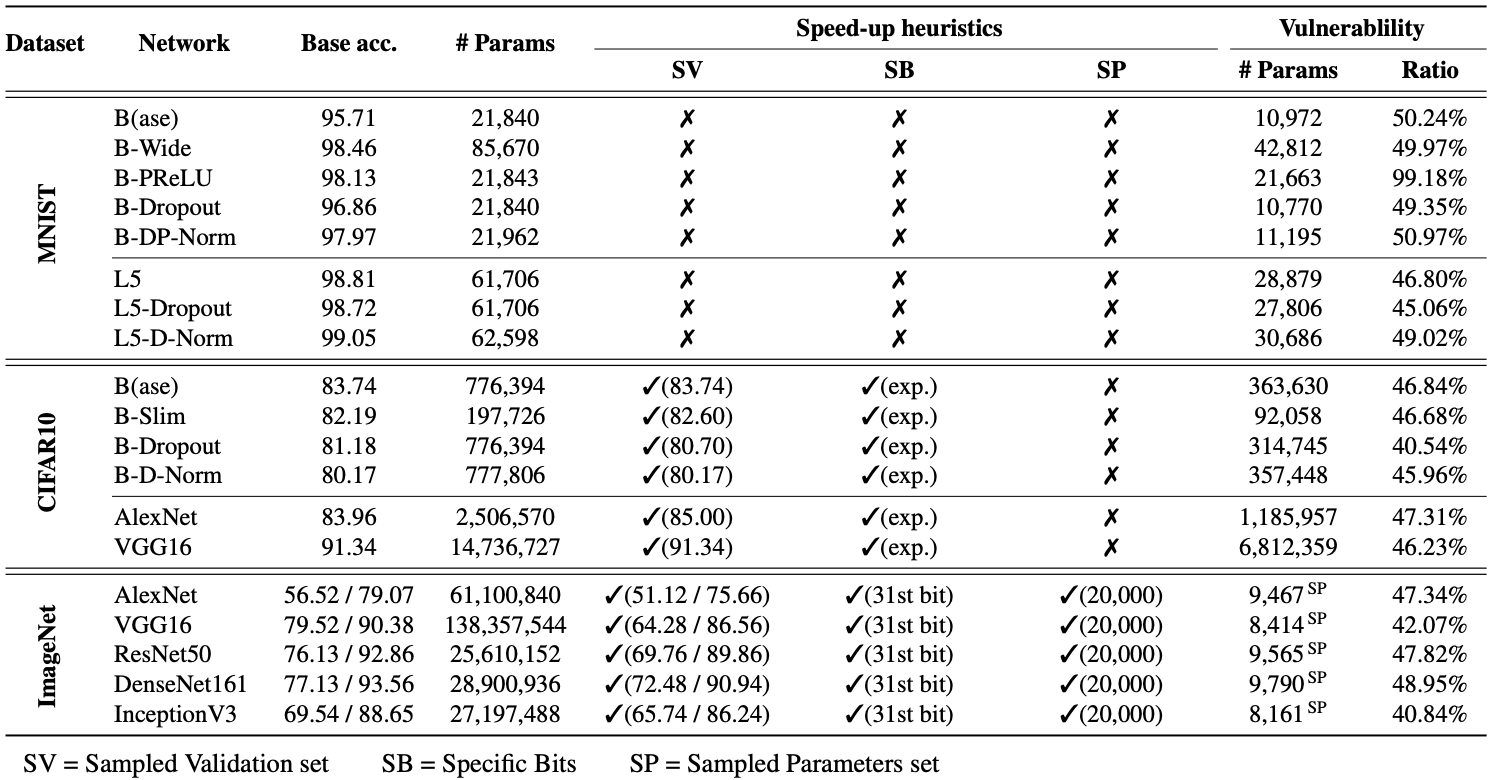
Note that SV, SB, and SP are the speed-up heuristics (refer to our paper for details). We use those heuristics for the CNN models trained on CIFAR-10 and ImageNet as those models contain millions of parameters to examine. For instance, VGG16 has 138M parameters, and its examination could take 942 days in a single CPU environment ~ 3 years (an endless Ph.D. study).
Surprisingly! Our results showed that in all 19 CNNs, 40~99% parameters include at least one Achilles bit. We also found that a model has at least one bit that causes “Terminal Brain Damage” — i.e., the MaxRAD becomes 99% when the bit is flipped. This is far below one can expect as the randomly initialized classifier’s accuracy on a CIFAR-10 model is around 10%. Moreover, we also found the number of vulnerable parameters varies in different architectures.
Interesting! Can You Tell Me What Are the Factors Contributing to This?
Sure, we began investigations on the factors that may contribute to the vulnerability. In particular, we focus on a parameter’s bitwise representations and DNN-level properties:
[Summary: Impact of the Bitwise Representation]
- Mostly, Achilles bits exist in the exponent of the IEEE-754 format (24-31st bits)
- Mostly, the 0 to 1 direction of a bit-flip contributes to the vulnerability.
- Most Achilles bits are in the positive parameters, not in negative parameters.
[Summary: Impact of the DNN-level Properties]
- Increasing the width of a network leads to the increase of vulnerable parameters, proportionally. (See: MNIST-Base vs. MNIST-B-Wide)
- Using the activation function that allows negative activations can double the vulnerability of a network to a single bit-flip (See: MNIST-Base vs. MNIST-B-PReLU)
- Common training techniques that reduce the dependence of a DNN’s decision on a small set of parameters, e.g., Dropout or Batch-normalization, cannot reduce this vulnerability. (See: MNIST-B-Dropout vs. MNIST-B-D-Norm)
- A DNN architecture containing components unused in inference can decrease the vulnerability of a DNN to a single bitwise corruption (See: AlexNet vs. InceptionV3)
For more details, we highly encourage readers to look at our paper.
Separately, our paper examines two distinct attack scenarios where the community has a lot of interests: transfer learning and targeted misclassification cases. Here, we also had several interesting findings. First, we found that Achilles bits transfer; those bits in a teacher model can still lead to a significant accuracy drop of a model when they are flipped in the student model. Second, there are also bits in a DNN that show an interesting behavior. Once the bit flips, it doesn’t cause a significant accuracy drop, but they can cause targeted misclassifications of a specific set of samples, which can be used for the targeted misclassifications.
Okay, Then How Can an Adversary Exploit This Vulnerability?
Let’s start thinking about who’s our attacker.
- Capability-wise: Surgical and blind attackers. A surgical attacker can flip the bit in an intended location in memory, e.g., the attacker can only flip the 31st-bit (MSB) whereas the blind attacker doesn’t have fine-grained control over the bit-flips. The blind attacker is completely unaware of where bit-flips land in memory.
- Knowledge-wise: Black-box and white-box settings. A white-box attacker knows the victim model, at least partially; thus, she can analyze where the vulnerable parameter locations would be in memory. But, the black-box attacker doesn’t.
Then, we illustrate those attackers in the figures below:
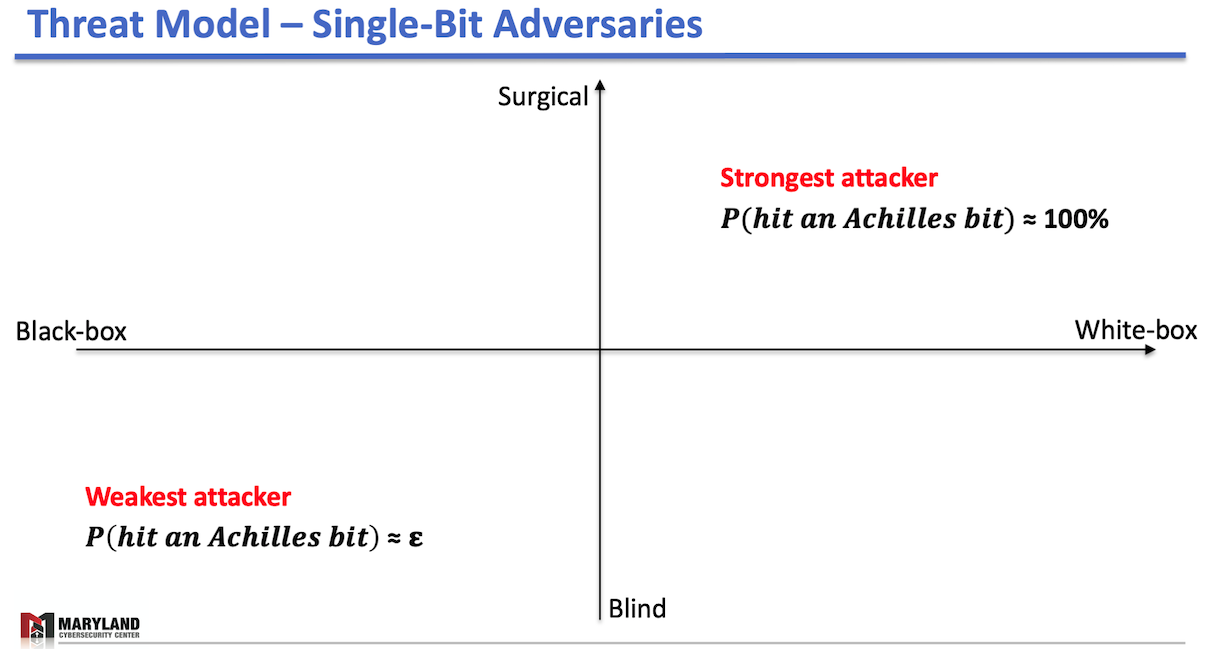

In the left figure, the strongest attacker is in the right-top corner; a surgical attacker in the white-box setting who can flip any bits in an intended location in memory. This attacker is omnipotent; one can deliberately tune the attack’s inflicted accuracy drop—from minor to catastrophic damage. Besides, the attacker can force the victim DNN to misclassify a specific set of samples without causing any significant accuracy drop over the test-set.
On the opposite hand, there’s the weakest attacker who doesn’t know which bit to flip and cannot control the bit-flip locations in memory. This attacker has a low probability of hitting an Achilles bit (less than epsilon). For example, in VGG16, the chance becomes 1.32%. Worth mentioning that the blind attacker gains no significant advantage over the white-box settings as the lack of capability prevents the attacker from acting on the knowledge of the victim model.
However, one surprising observation we had (in the right figure):
Our Practical Weapon: Rowhammer
[TL;DR] Rowhammer: if an adversary accesses certain memory locations repeatedly, the attacker can induce bit-flips to the neighboring locations that may contain the victim’s data.
[1 min ver.] Rowhammer [2] is a software-induced fault attack that provides the attacker with a single-bit corruption primitive to specific physical memory (DRAM) locations. That is, an attacker capable of performing specific memory access patterns can induce persistent and repeatable bitwise corruptions from the software. Since our purpose is to test the resiliency of DNN models against bitwise corruption, Rowhammer represents the perfect candidate for our task.

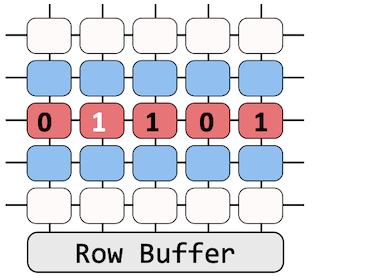
[3 min ver.] Let’s take a look at how Rohammer works (see the figures above). The left figure depicts a DRAM bank structure; a bank is a bi-dimensional array of memory cells connected to a row buffer. You can simply consider it like: each square (a cell) contains data (0 or 1), and the cell has a capacitor whose charge determines the value of a specific bit in memory. When we read the data from DRAM, a read command is issued to a specific row. Then, the row becomes activated, which means that its contents will be transferred to the buffer, and a requested CPU will read it. Activation is often requested (refresh) as the capacitors leak charges over time.
Rowhammer exploits this activation behavior by frequently reading neighboring rows. In the right figure, we illustrate “How”. Suppose that the victim’s data is stored in a row (red cells) enclosed between the two neighboring rows (blue cells). If an adversary repeatedly accesses the blue rows, due to the continuous activations, the victim’s data is under intense duress. In consequence, there exists a large probability of bitwise corruptions on its content.
Interesting, But Is Rowhammer A Practical Threat?
[MLaaS scenarios] Our work also considers a cloud environment where the victim’s deep learning system is deployed inside a VM (or a container) to serve the requests of external users. For making test-time inferences, the trained DNN model and its parameters are loaded into the system’s (shared) memory and remain constant in normal operation. Recent studies describe this as a typical scenario in Machine-Learning-as-a-Service. Under this setting, it has been shown that an adversary can simply spin-up a VM that runs on the same host as the victim’s (co-location) and is able to cause bit-flips in the victim machine’s memory [3, 4].
[Let’s do attacks] Our analysis focuses on the blind, black-box attacker since the surgical, white-box attacker is already omnipotent. We constructed a simulated environment where we run a Python process that constantly queries the VGG16 model trained on ImageNet, and another process (an attacker) tries to induce bit-flips to the Python process memory. Due to our attacker’s blindness about bit-flip locations, the attack consequences can be:
- We hit an Achilles bit (the accuracy drop over 10%)
- We cause a process crash (our attack is detected)
- We hit any bit that doesn’t lead to significant damage.
To quantify the impact of Rowhammer attacks, we use the HammerTime [5] database that contains the vulnerable bit locations in 12 different DRAM chips (Note that we define the vulnerability of a DRAM based on the number of vulnerable bits in DRAM). Yeah, this setting allowed us to systematically quantify our attack’s consequences, not just observing one case of exploitation. We conducted 25 experiments for each of 12 DRAM chips, and each experiment is composed of 300 cumulative bit-flip attempts. And Ta-Da!
[Our analysis results] A blind attacker can induce the “Terminal Brain Damage” to the victim model effectively and inconspicuously. The inconspicuousness comes from the fact that we only observe six crashes over the entire 7500 bit-flip attempts (0.08% crash rate).
- On average: 62% of our 7500 bit-flip attempts, the attacker can hit an Achilles bit.
- Most vulnerable DRAM chip: 96% of the attempts led to the accuracy drop > 10%.
- Least vulnerable DRAM chip: The attacker has only 4% of successes over 7500 runs.
[Implications]
- The blind Rowhammer attacker is a practical threat against DNNs running in the cloud.
- Contrary to the most previous attacks, this blind attacker doesn’t need to flip a specific bit (such as the page permission bit) as a DNN model contains many Achilles bits.
More Practicality Evaluations Are in Our Paper!
Our paper also evaluates the surgical, white-box attacker, who can flip bits in the intended locations in memory. Since this attacker is able to cause any possible outcomes, our analysis focuses more on how an attacker can exactly flip a bit in an intended location. This includes a set of primitives such as memory templating, searching for vulnerable templates, and memory massaging that enables the attacker to place a DNN in the memory location where she wants.
[Credits] Our team has experts in Rowhammer research (shout out to Pietro Frigo and Prof. Cristiano Giuffrida from Vrije Universiteit Amsterdam!). During this research, we couldn’t have our Rowhammer contributions without their well-through-out comments and feedback.
Scary, Can We Think of Any Defense Mechanisms?
Yes, we can. Our paper discussed two directions towards making DNNs resilient to bit-flips:
- Restrict activation magnitudes via specific activation functions like ReLU6.
- Use low-precision numbers; for example, compressing a DNN with 8-bit quantization.
We think system-level Rowhammer defenses wouldn’t be a silver-bullet. First, they often require specific hardware support. Second, they have not been widely deployed since system-level defenses require infrastructure-wide changes from cloud host providers. Third, even if the infrastructure is resilient to Rowhammer attacks, an adversary can leverage other vectors to exploit bit-flip attacks for corrupting a model. As a result, our discussion is to find the solutions that can be directly implemented on the defended DNN model. For more details, we recommend our readers to look at Sec. 6 in our paper.
Resources
Our post summarizes the results in our USENIX Security 2019 paper “Terminal Brain Damage: Exposing the Graceless Degradation in Deep Neural Networks under Hardware Fault Attacks”
- Our USENIX’19 paper is in [arXiv].
- You can find our USENIX presentation on [YouTube].
- We will upload the code for our experiments on Github soon.
Acknowledgement
Thanks to our collaborators for their feedback on a draft and their contributions to the materials.
References
[1] Lecun et al., Optimal Brain Damage, NeurIPs 1990. [PDF]
[2] Kim et al., “Flipping Bits in Memory Without Accessing Them: An Experimental Study of DRAM Disturbance Errors”, ISCA 2014. [PDF]
[3] Bosman et al., “Dedup est machina: Memory deduplication as an advanced exploitation vector” IEEE S&P 2016. [PDF]
[4] Xiao et al., “One Bit Flips, One Cloud Flops: Cross-VM Rowhammer Attacks and Privilege Escalation” USENIX Security 2016. [PDF]
[5] Tartar et al., “Defeating Software Mitigations against Rowhammer: a Surgical Precision Hammer” RAID 2018. [PDF]