Program 3

Deterministic Finite-State Automata

A deterministic finite-state automaton (DFA) is an abstract machine that has the following job: read in a sequence of symbols, and decide whether or not that sequence of symbols is "in the language" or not. For example, consider the "language" consisting of just the following very, very simple noun phrases:

the man
the tall man
the tall tall man
the tall tall tall man
etc.

This may not seem like much of a language (it's got a vocabulary of three words, and no verbs) but it's good enough for illustrative purposes! Here is a DFA -- represented as a graph -- that decides whether or not a sequence of input symbols is in this language.

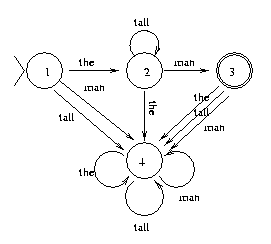
Example DFA

How They Work

Here's how it works. Let's suppose we have the input sequence (the tall man). First, you start out in the "initial state"; this is state 1, as indicated graphically by the carat-like annotation to its left. Next, you read the next symbol in the input and follow the corresponding arc to the next state: from state 1, with input the, the diagram says you go to state 2. (This is also known as "following the transition" to the next state.) You've "read in" that first symbol, so at this point the remaining input contains (tall man). Since there's still input left to read, you do the same thing over again: reading tall and taking the appropriate transition, which in this case leads you right back to state 2. Now the remaining input contains (man). Once again you follow the same process: in this case reading man in state 2 leads you to state 3.

At this point, you've read all the symbols in the input. Now, some of the states in the machine are "final states," indicated by a double circle; in this machine there's just one, namely state 3. Once you've exhausted the input, you look at the state you ended up in. If it's a final state, then the machine accepts the input -- that is, it says "yes, the input is in the language". If it's not a final state, the machine rejects the input -- that is, it says "no, the input is not in the language". Try tracing through the same process as above with the input (the tall the man) and you'll wind up in state 4, which is not a final state.

Notice that no matter what state you're in, the diagram of the machine always has exactly one destination state for every symbol in the vocabulary -- never zero, and never more than one -- and also notice that that you can never just jump from one state to the other without reading in any of the input. These things are what make the machine deterministic, since at any point in time the machine's next step is completely determined.

Representing a DFA in LISP

Stated a little more formally, a DFA is a 5-tuple consisting of the following:

An "alphabet", i.e. a set of symbols it knows about
A set of states
Exactly one initial state
A (possibly empty) set of final states
A set of transitions, each of the form (s1 symbol s2), satisfying the conditions for DFA's in the above paragraph.

Here's a convenient representation of the above machine as a 5-tuple in a LISP notation:

 ((ALPHABET       (man tall the))
  (STATES         (1 2 3 4))
  (INITIAL-STATE  1)
  (FINAL-STATES   (3))
  (TRANSITIONS    ((1 man 4) (1 tall 4) (1 the 2)
		   (2 man 3) (2 tall 2) (2 the 4)
		   (3 man 4) (3 tall 4) (3 the 4)
		   (4 man 4) (4 tall 4) (4 the 4))))

Note that some parts of this representation may not be needed in your program, but are included because 5-tuples are the formal way DFA's are specified.

The Assignment

Your job is to write a function called accepts that takes two arguments: a list of symbols and a DFA represented as above. Calling the function should return t (true) if the DFA accepts the sequence of symbols (i.e. the sequence is "in the language" of the DFA), and should return nil otherwise.

That is, if the above DFA were the value of symbol +dfa2+ you should get:

 * (accepts '(the tall man) +dfa2+)
 T

 * (accepts '(the tall tall tall man) +dfa2+)
 T

 * (accepts '(the tall the man) +dfa2+)
 NIL

 * (accepts '() +dfa2+)
 NIL

Another DFA

Here's another DFA, whose alphabet (vocabulary of symbols) is even simpler: just the symbols a and b. It accepts the language that consists of sequences of a single a, followed by an even number of b's (possibly zero of them), followed by a final a. This example illustrates how to define a global variable in your programs, in this case a global variable called +dfa1+.

 (defconstant +dfa1+
   '((ALPHABET        (a b))
     (STATES          (1 2 3 4 5))
     (INITIAL-STATE   1)
     (FINAL-STATES    (4))
     (TRANSITIONS     ((1 a 2) (1 b 5)   
		       (2 a 4) (2 b 3)   
		       (3 a 5) (3 b 2)   
		       (4 a 5) (4 b 5)   
		       (5 a 5) (5 b 5))))
   "A deterministic finite-state automaton that accepts the language
    {(a b^n a), n is an even number}, i.e. {(a a), (a b b a), (a b b
    b b a), ...}."
 )

You'll be using this DFA to test your program once you've completed writing it.

Hints

Unlike in previous assignments, you are not being given step-by-step building blocks for this program. That means that your first step should be to look at the problem and understand what the program is supposed to do, e.g. working it through by hand for several different inputs.

Your second step should be to break the problem down into smaller pieces. What are some smaller, easier functions you're sure you will need? Create names for them and decide roughly what their inputs and outputs will be, but don't implement them yet. You shouldn't implement anything until you've got the problem mapped out.

The next step should be to look at the top level problem you're solving. What kind of "feel" does it have -- recursive? applicative? (It might well have an iterative feel, but we haven't covered iterative programming yet so that's not an option.) If the top level seems recursive, what does the base case look like (or cases, if there's more than one)? How do you break the problem into the three pieces that Touretzky describes: base case, single step, smaller journey? (If you're of a mind to try Touretzky's recursion templates, go ahead, though if the problem is hard to squeeze into the template you've chosen it may be because you've chosen the wrong one.) If there's applicative programming involved, what functionality are you applying to what list, to get what result?

Based on your breaking down of the top level, start sketching out some function definitions, though perhaps not in full detail: even without completely specifying the insides, what arguments does a function take, and what value does it return? If there's recursion or application involved, trace manually through function calls, following the input/output behavior you've specified; start with the small, easy cases, and work your way up to something more complicated. This process may lead you to change the arguments or values or behavior of functions, or to add or get rid of functions. Ultimately go back to the top and try manually tracing through things again with a different input.

Finally, start programming. If you've got easy little helper functions, write them first, and test them before moving on, first trying the simplest cases and then doing more complex ones. Then go back and work from the top level, implementing the approach you've worked through on paper. Implement things partially and test them as you go along, always making sure that your functions do what they should on the small or easy cases before moving on. If there's recursion involved, trace the recursive function so you can see what its inputs and outputs are when it gets called.

If you get wedged (that's the technical term!), take a break. Even five minutes away from the problem doing something else (reading news, surfing the Web, sending me hate mail) is often enough to get you out of am mental rut, letting you see a different path or possibility when you return.

Turning in the Assignment

Please let me have hardcopies of the code you've written, as well as the output you get when you test your code using the following:


 (mapcar #'(lambda (x) (accepts x +dfa1+)) 
	 '(() (a) (b) (a a) (a b) (b a) (b b) 
           (a b a) (a b b) (a b b a)))

Good luck, and have fun!