Hal Daume III (
 )
)
Second Release 24 January 2005
First Release 20 August 2004 -- go here
 )
)
Maximum entropy models are very popular, especially in natural language processing. The software here is an implementation of maximum likelihood and maximum a posterior optimization of the parameters of these models. The algorithms used are much more efficient than the iterative scaling techniques used in almost every other maxent package out there. A description of the algorithms is available in the following unpublished report:
There are several changes from version 1 to version 2. First, some limits (number of examples) has been raised to over four million (and it's still more than sufficiently efficient with this much data). Additionally, features have been added for "density estimation" style modeling (specifically for whole-sentence maximum entropy language models), restarted training, naive domain adaptation and feature selection. See options -prog/-sfile, -mean, -init and -abffs below.
The software can be downloaded as source code (in O'Caml) or as executables for i686 Linux or Sun4 Solaris. For executables, there are both debugging versions and optimized versions avaiable:
Source: megam_src.tgz
Linux: Debugging: megam_i686.gz or Optimized: megam_i686.opt.gz
Solaris: Debugging: megam_sun4.gz or Optimized: megam_sun4.opt.gz
Windows: Debugging: megam.exe or Optimized: megam_opt.exe (may require CygWin)
For people at ISI: The optimized executables can be run as /nfs/isd3/hdaume/bin.i686/megam or /nfs/isd3/hdaume/bin.sun4/megam, depending on your platform.
This code is free to anyone and you can use it in any research thing you want. For commercial use, please contact me. If you use it for work in a published article, please add a footnote acknowledging the software, or cite the article above.
I have produced some graphs comparing the efficiency of MegaM to YASMET, a maxent software package by Franz Josef Och (now at Google), that uses generalized iterative scaling for optimization. This has been done both for a binary problem and a multiclass problem, each with about 140 thousand training instances and 30 thousand test instances, with hundreds of thousands of features (an NP chunking task, if you must know).
Below, we see training error and test error curves plotted against time (not number of iterations) for GIS and for CG (our binary optimizer). Both are done with lambda=1 smoothing. As you can see, CG both achieves lower error rates, and achieves them more quickly (it is done after less than 100 seconds, less than the time it takes YASMET to even start up):
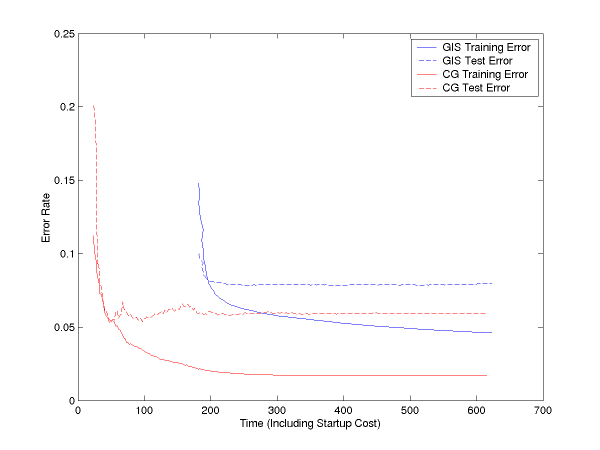
If you subtract off the startup file reading time, the curves are:
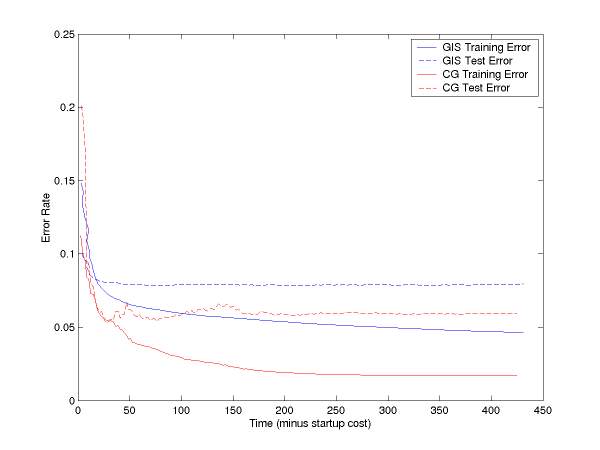
We have done the same thing for multiclass. In this, we have two versions of LM-BFGS, one which uses explicit feature vectors and one which uses implicit feature vectors (see usage and file formats below). Both are faster than GIS, and implicit is quite significantly faster:
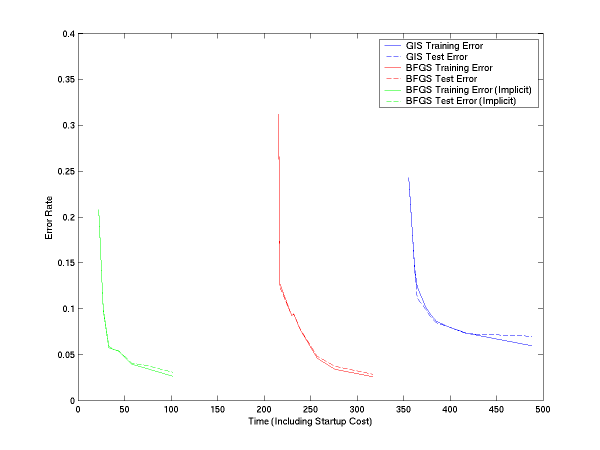
If you subtract off the startup file reading time, the curves are:
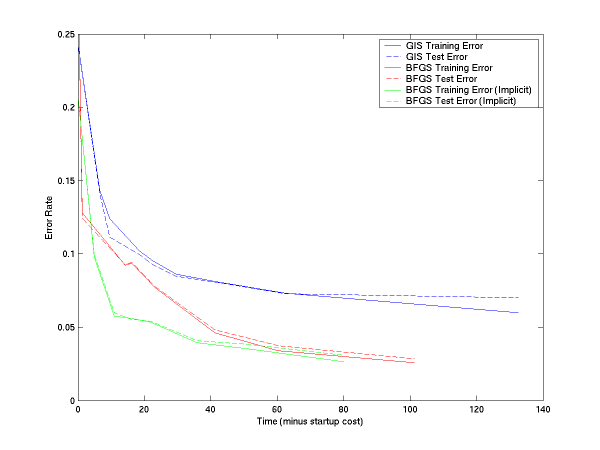
The MegaM software lists its usage if you run it with no (or with invalid) arguments. Three types of problems can be solved using the software: binary classification (clases are 0 or 1), binomial regression ("classes" are real values between 0 and 1; the model will try to match its predictions to those values), or multiclass classification (classes are 0, 1, 2, and so on).
usage: megam [options]A standard call for optimization would be something like "megam binary file" or "megam multiclass file where file is an existing file that contains the training data (see file formats, below). This will run for at most 100 iterations (for BFGS, when the weight vector doesn't change, iterations will cease no matter what you specify).[options] are any of: -fvals data is in not in bernoulli format (i.e. feature values appear next to their features int the file) -explicit this specifies that each class gets its own feature vector explicitely, rather than using the same one independently of class (only valid for multiclass problems) -quiet don't generate per-iteration output -maxi <int> specify the maximum number of iterations (default: 100) -dpp <float> specify the minimum change in perplexity (default: -99999) -memory <int> specify the memory size for LM-BFGS (multiclass only) (default: 5) -lambda <float> specify the precision of the Gaussian prior (default: 1) -tune tune lambda using repeated optimizations (starts with specified -lambda value and drops by half each time until optimal dev error rate is achieved) -sprog <prog> for density estimation problems, specify the program that will generate samples for us (see also -sfile) -sfile <files> for de problems, instead of -sprog, just read from a (set of) file(s); specify as file1:file2:...:fileN -sargs <string> set the arguments for -sprog; default "" -sspec <i,i,i> set the <burn-in time, number of samples, sample space> parameters; default: 1000,500,50 -sforcef <file> include features listed in <file> in feature vectors (even if they don't exist in the training data) -predict <file> load parameters from <file> and do prediction (will not optimize a model) -mean <file> the Gaussian prior typically assumes mu=0 for all features; you can instead list means in <file> in the same format as is output by this program (baseline adaptation) -init <file> initialized weights as in <file> -abffs <int> use approximate Bayes factor feature selection; add features in batches of (at most) <int> size <model-type> is one of: binary this is a binary classification problem; classes are determined at a threshold of 0.5 (anything less is negative class, anything greater is positive) binomial this is a binomial problem; all values should be in the range [0,1] multiclass this is a multiclass problem; classes should be numbered [0, 1, 2, ...]; anything < 0 is mapped to class 0 density this is a density estimation problem and thus the partition function must be calculated through samples (must use -sprog or -sfile arguments, above)
The program will write the learned weights to stdout and will write progress reports to stderr. For instance, using the small2.gz data set (unzip it first), we get (with stdout is directed to another file or to /dev/null):
% ./megam.opt multiclass small2 > weights Scanning file...1000 train, 600 dev, 700 test, reading...done it 1 dw 3.162e-01 pp 1.09651e+00 er 0.44500 dpp 1.08996e+00 der 0.45000 tpp 1.10488e+00 ter 0.44714 it 2 dw 2.409e-01 pp 7.36678e-01 er 0.17100 dpp 7.05990e-01 der 0.15667 tpp 7.48023e-01 ter 0.17571 it 3 dw 2.620e-01 pp 4.58951e-01 er 0.08500 dpp 4.33894e-01 der 0.06667 tpp 4.65503e-01 ter 0.08857 it 4 dw 2.439e-01 pp 3.20783e-01 er 0.05800 dpp 3.05617e-01 der 0.05500 tpp 3.24992e-01 ter 0.05429 it 5 dw 3.763e-01 pp 2.19297e-01 er 0.03100 dpp 2.05452e-01 der 0.03167 tpp 2.21807e-01 ter 0.02429 it 6 dw 4.723e-01 pp 1.70574e-01 er 0.01300 dpp 1.64530e-01 der 0.01500 tpp 1.72357e-01 ter 0.00857 it 7 dw 2.124e-01 pp 1.46320e-01 er 0.01700 dpp 1.36616e-01 der 0.01500 tpp 1.52102e-01 ter 0.01714 it 8 dw 2.558e-01 pp 1.18902e-01 er 0.01000 dpp 1.12224e-01 der 0.01167 tpp 1.22858e-01 ter 0.00571 it 9 dw 3.500e-01 pp 1.03973e-01 er 0.00800 dpp 9.84038e-02 der 0.01000 tpp 1.07186e-01 ter 0.00429 it 10 dw 1.806e-01 pp 8.78036e-02 er 0.00500 dpp 8.35916e-02 der 0.00667 tpp 9.10291e-02 ter 0.00286 it 11 dw 9.880e-02 pp 7.99700e-02 er 0.00300 dpp 7.63937e-02 der 0.00333 tpp 8.27229e-02 ter 0.00286 it 12 dw 5.143e-01 pp 6.30349e-02 er 0.00100 dpp 6.01651e-02 der 0.00167 tpp 6.45565e-02 ter 0.00143 it 13 dw 1.995e-01 pp 6.02724e-02 er 0.00100 dpp 5.76503e-02 der 0.00167 tpp 6.10948e-02 ter 0.00143 it 14 dw 3.905e-01 pp 5.64137e-02 er 0.00000 dpp 5.32447e-02 der 0.00000 tpp 5.69302e-02 ter 0.00000 it 15 dw 4.482e-02 pp 5.64692e-02 er 0.00000 dpp 5.32684e-02 der 0.00000 tpp 5.69913e-02 ter 0.00000 it 16 dw 4.023e-02 pp 5.63336e-02 er 0.00000 dpp 5.31459e-02 der 0.00000 tpp 5.68540e-02 ter 0.00000 it 17 dw 2.566e-01 pp 5.56057e-02 er 0.00000 dpp 5.24170e-02 der 0.00000 tpp 5.60241e-02 ter 0.00000 it 18 dw 2.695e-01 pp 5.57867e-02 er 0.00000 dpp 5.26410e-02 der 0.00000 tpp 5.61494e-02 ter 0.00000 it 19 dw 9.443e-02 pp 5.53901e-02 er 0.00000 dpp 5.23822e-02 der 0.00000 tpp 5.56894e-02 ter 0.00000 it 20 dw 1.356e-01 pp 5.52823e-02 er 0.00000 dpp 5.22328e-02 der 0.00000 tpp 5.56007e-02 ter 0.00000 it 21 dw 2.865e-01 pp 5.42961e-02 er 0.00000 dpp 5.13820e-02 der 0.00000 tpp 5.46883e-02 ter 0.00000 it 22 dw 0.000e+00 pp 5.42961e-02 er 0.00000 dpp 5.13820e-02 der 0.00000 tpp 5.46883e-02 ter 0.00000The first line tells us how much data it has read (1000 training instances, 600 development instances and 700 test instances). Then, for each iteration, it gives us the iteration number, the maximum absolute weight change and, for each of training, development and test, the current average perplexities and error rates. It automatically stopped after 22 iterations because dw has dropped to zero.
If we look at the beginning of the file weights, we get:
**BIAS** 0 -0.57549 -0.72752 -0.35552 1.10426 CLASSBEGIN 0 0.20725 0.11234 0.43943 1.73593 Begin_WORD_Confidence 0 0.00257 -0.05196 0.06445 -0.00055 Begin_LCWORD_confidence 0 0.00257 -0.05196 0.06445 -0.00055 Begin_STEMWORD_confid 0 0.00257 -0.05196 0.06445 -0.00055The first column is the feature name and then each remaining column is the feature weight for that class number (in this case, class zero through four). The weights for the first class are always zero.
Using this weight vector, we can predict new data:
% ./megam.opt -predict weights multiclass small2 | head -5 Scanning file...1000 train, 600 dev, 700 test, reading... 3 0.0013275 0.0011296 0.160847 0.810167 0.026528 4 0.0000278 0.0002604 0.001853 0.000602 0.997256 0 0.9961875 0.0000467 0.000001 0.002647 0.001116 2 0.0000024 0.0119139 0.981444 0.005073 0.001565 4 0.0000499 0.0006470 0.005878 0.003062 0.990362 Error rate = 0 / 2300 = 0The first and last line are written to stderr; the predictions are to stdout. The first column is the predicted class, and then each other column is the corresponding class probabilities. The lines to stdout are produced lazily (i.e., it doesn't read in the whole file before producing them).
For binary problems, things are pretty much the same:
% ./megam.opt -maxi 10 binary small2 > weights_b Scanning file...1000 train, 600 dev, 700 test, reading...done it 1 dw 5.773e-01 pp 4.07447e-01 er 0.17400 dpp 4.14512e-01 der 0.18500 tpp 4.06262e-01 ter 0.17143 it 2 dw 2.407e+00 pp 2.24630e-01 er 0.04200 dpp 2.11013e-01 der 0.03167 tpp 2.30537e-01 ter 0.05000 it 3 dw 4.119e-01 pp 1.58570e-01 er 0.05600 dpp 1.50339e-01 der 0.05167 tpp 1.63930e-01 ter 0.05857 it 4 dw 2.802e+00 pp 1.00245e-01 er 0.01800 dpp 9.34123e-02 der 0.01500 tpp 1.06694e-01 ter 0.02143 it 5 dw 6.906e-01 pp 7.01913e-02 er 0.01100 dpp 6.59932e-02 der 0.01167 tpp 7.54798e-02 ter 0.01143 it 6 dw 1.486e+00 pp 4.93540e-02 er 0.00600 dpp 4.54756e-02 der 0.00333 tpp 5.32310e-02 ter 0.00714 it 7 dw 2.641e-01 pp 4.18101e-02 er 0.00600 dpp 3.93453e-02 der 0.00500 tpp 4.45824e-02 ter 0.00571 it 8 dw 1.987e+00 pp 2.51785e-02 er 0.00100 dpp 2.40243e-02 der 0.00167 tpp 2.70933e-02 ter 0.00143 it 9 dw 4.343e-02 pp 2.36266e-02 er 0.00100 dpp 2.26068e-02 der 0.00167 tpp 2.52784e-02 ter 0.00143 it 10 dw 2.440e-01 pp 2.04603e-02 er 0.00000 dpp 1.94030e-02 der 0.00000 tpp 2.19021e-02 ter 0.00000 % ./megam.opt -predict weights_b binary small2 | head -5 Scanning file...1000 train, 600 dev, 700 test, reading... 1 0.96136740922988028757 1 0.99935467626564855603 0 0.00228306268828848066 1 0.99992604373213311852 1 0.99945875141819140453 Error rate = 6 / 2300 = 0.0026087Here, it has mapped any class >0.5 to class +3 and anything less than 0.5 to class 0 (so class 0 is still class 0, and all of the classes 1,2,3,4 have become class 1). There are only two columns this time, corresponding to the class and its probability. The weight file looks a bit different, too:
**BIAS** 1.4162197 CLASSBEGIN 1.4162197 Begin_WORD_Confidence 0.0071583 Begin_LCWORD_confidence 0.0071583 Begin_STEMWORD_confid 0.0071583Since there are only two classes, and hence only one weight vector, you only get two columns, one for the feature name and one for the corresponding weight (for class 1).
If you try to use a multiclass weight vector with a binary problem, or vice versa, strange things will happen, so be careful (most likely, it will die).
Specifying a different value for maxi changes the number of iterations, putting dpp at, for instance, 0.00001 means that if the change in (training) perplexity drops below 0.00001, the algorithm will terminate. lambda is the precision of the Gaussian prior on the weights, 0 means no prior, 1000000 means too much prior. You can tune the lambda value by setting a maximum value using -lambda and specifying -tune, which will search for a good one by halfing lambda in a sequence of iterations until development error rate ceases to decrease.
There are roughly four file formats that are acceptable to MegaM. No matter what, each instance gets its own line and the first column (space or tab separated) is the class. For binary problems, this should be 0 or 1 (anything less than 0.5 goes to 0 and anything greater goes to 1). For binomial problems, this should be between 0 and 1 (anything less than 0 goes to 0 and anything greater goes to 1). For multiclass problems, this should be greater than zero (anything less than zero goes to zero).
In the simplest file format, the so-called "bernoulli implicit" format, after the class label, feature names are simply listed. It is called "bernoulli" because features can take only values of 0 or 1, and any non-present feature is assume to have value 0. It is called implicit because, for multiclass problems, we assume the same feature vector for all class labels. An example is:
0 F1 F2 F3 1 F2 F3 F8 0 F1 F2 1 F8 F9 F10The second simplest file format, "non-bernoulli implicit" requires that the option -fvals be specified to the program. In this, feature values are written adjacent to their feature names. The values can be any real number. An identical example would be:
0 F1 1.0 F2 1.0 F3 1.0 1 F2 1.0 F3 1.0 F8 1.0 0 F1 1.0 F2 1.0 1 F8 1.0 F9 1.0 F10 1.0But of course the 1.0s could be anything.
The "explicit" file formats are only for multiclass problems and are useful (supposedly) if different features fire depending on the class label. In this case, we need to specify a feature vector for each possible class; these are separated by space-delimited pound signs. For instance:
0 # F1_C0 F2_C0 F3_C0 # F1_C1 F2_C1 F3_C1 # F1_C2 F2_C2 F3_C2 1 # F2_C0 F3_C0 F8_C0 # F2_C1 F3_C1 F8_C1 # F2_C2 F3_C2 F8_C2 2 # F1_C0 F2_C0 # F1_C1 F2_C1 # F1_C2 F2_C2In this example, there are the same features (more or less) for each class, but the are given slightly different names. This need not be the case: you can put anything you want. When you use explicit files, you need to specify -explicit to the program. You can use both explicit and non-bernoulli files by specifying -explicit and -fvals on the command line and using the obvious corresponding file format. Note that when you use explicit format, the weight vector output will not have a different column for each class; it will simply have each feature with a single weight.
Finally, you can break your training file into a training, development and test section. The first segment of the file is automatically training data (what is used to optimize the weights). If you then have a single line with the word DEV, then what follows will be considered development data (what is used to optimize the lambda parameter). Finally, a single line with the word TEST specifies that the remainder of the file is test data, which is (understandably) not used for any optimization.
To use the density estimation capabilities, you must provide independent samples from a base distribution (typically an n-gram language model). See the Chen/Rosenberg paper on whole sentence maxent language models for more details. You still need training data, which should consist only of "positive examples (labeled however you like; with zeros is best). You then must tell us how to generate samples. This can either be done by providing a file that has one sample per line (in the same format as the training data), or by providing the name of a program that will generate samples for us. In the latter case, the program should take (at least) two arguments: first, the file name to dump the samples to; second, the number of samples to generate. In the case of a file, just specify the file name.
You will additionally need to set the sample spects (-sspec #,#,#) where the three comma-separated numbers are the burn-in time, the number of samples to use, and how far apart to space the samples (we use an independence sampler). Finally, if the samples might contain features not in the training data and you don't want these to be ignored, list them all in a file and provide this as an option to -sforcef and it will include all the features.
We provide capabilities to do naive domain adaptation as described by Chelba and Acero in their 2004 EMNLP paper. The idea is to use the weights learned from an "out of domain" corpus as the prior means for the "in domain" data. There are therefore two steps to doing such training. First, use your out of domain data to train a model and same the model file. Now, use the in domain data to train a new model, but use the -mean parameter to specify the model output from the out of domain data. This tends to give better performance to other options and is quite trivial to run.
The optimization problem we solve is convex and so there's a unique maximum, but sometimes getting there is slow. If you have a good guess at paramters, or you want to initialize them to something other than zero, write the parameters to a file in the same format as model outputs and the use the -init command to load them. This is also useful if you want to just run more iterations.
Our last "cool" capability is to do feature selection using approximate Bayes factors (see my paper on this topic). This is reasonably efficient, but not for huge huge data sets. To use it, simply specify -abffs # as an option, where # is the number of features that should be added each iteration. I typically use 50, but YMMV. Using 1 is "correct", but using more isn't too bad and is much more efficient.
Sometimes you would like to weight different examples are more or less "important" than others. To do so, simply place the string "$$$WEIGHT #" immediately following the class number for the corresponding example, where # is a positive real number. For instance, saying "$$$WEIGHT 2" is equivalent to simply including two identical lines without weight (but will be slightly more efficient).
